3分でちょっとだけわかる TPE

08 October, 2022 - 2 min read - Tags: Grasshopper,Tunny

はじめに

Grasshopper で使用できる最適化コンポーネント Tunny を開発しています。

food 4 Rhino - Tunny

その中でベイズ最適化や進化戦略、準モンテカルロなどこれまでの Grasshopper の最適化コンポーネントでなじみのないアルゴリズムがあります。それらを使うにあたってざっくりとしたアルゴリズムへの理解があるとより使いやすくなるため、簡単な紹介をします。

ここでの内容は Tunny の公式ドキュメントの Technical Info を翻訳したものがベースになります。

この記事では TPE という手法について紹介します。アルゴリズムのざっくりとした理解を目的にしており、正確でない可能性があります。詳細は最後に掲載している参考文献を確認してください。

Tree-structured Parzen Estimator(TPE)

TPE はベイズ最適化に分類される手法です。ベイズ最適化で検索すると TPE よりもガウス過程（GaussianProcess, GP）を使ったものが多くヒットします。ここでは簡単にそれらの相違点の概要を以下に示します。

GP は p(y|x) を使って期待改善量(ExpectedImprovement, EI)を計算します。
- 観測点から事後分布を計算し、それを使用して次の探索点を決定します。
- GP を実行する過程で逆行列計算があるため、時間オーダーは O(n^3) になります。
TPE は p(x|y) と p(y) を使用して EI を計算します。
- y の事後分布 p(y|x) は必要ありません。
- 1 変数当たりの TPE の時間計算量は O(nlogn) です。これは、y を y∗ の値で 2 分割することに関連して値をソートする必要があるためです。
- 各変数は (多変量ではなく) 独立していると想定されるため、全体の時間オーダーは上記に変数の数 d をかけて O(dnlogn) になります。

TPE のアルゴリズムについて

このセクションでは実際の TPE の動作について説明します。以下の STEP2 ～ STEP3 を繰り返し実行することで、TPE は最適化を行います。

ステップ 1

Tunny のデフォルト設定では、はじめに目的関数の代理モデル（サロゲートモデル）を作成するため、ランダムサンプリングが実行されます。ここでは、次の関数の最小化問題を例に解いていきます。

y = exp(x)*sin(3πx)
-1 < x < 1

サンプリングした結果は以下です。図中の ★ はサンプリングされた点です。

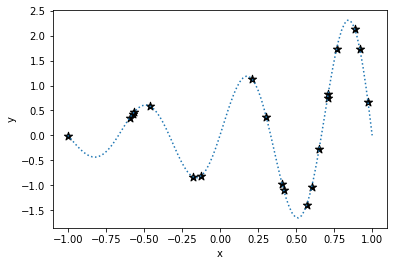
ステップ 2

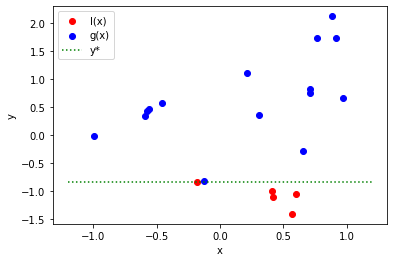
得られたサンプリング点を l(x) と g(x) の 2 つに分割します。 Tunny は分割するとき、y* というある値で分割します。 y* は上位 10％の個体または 25 個体の小さい方で分割する値になります。

次の例では y*=-0.83 となり、この値を使ってサンプリングされた点を l(x) と g(x) に 2 分します。

ステップ 3

次に、l(x) と g(x) のそれぞれに対してカーネル密度推定 (KernelDensityEstimator, KDE) を実行します。 KDE は、滑らかな曲線で表現された値のヒストグラムと考えることができます。次の図の棒グラフは l(x) と g(x) のヒストグラムを示し、曲線は KDE の結果です。

KDE によって推定される l(x) は、上位の個体 (つまり値が小さい個体) を得られる確率が高い x の値と考えることができます。同様に g(x) は、下位の個体 (つまり値が小さい個体) を得られる確率が高い x の値と考えることができます。

TPE では、l(x) と g(x) の比 l(x)/g(x) が最大となる x を見つけることによって、次の探索点が決定されます。この例では、x=0.455 になります。

l(x)/g(x) を最大化する点を探すことは上記の説明から、最も値が小さい個体を取得する確率が高く、かつ値が大きい個体を取得する確率が小さい点を TPE が計算することを意味します。

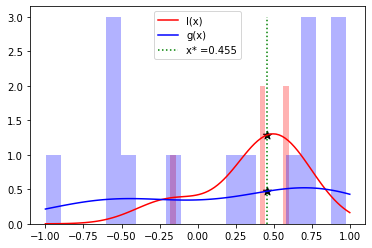
KDE は、TPE の「PE」部分の由来である Parzen Estimator としても知られています。

注意事項

STEP 1 はランダムサンプリングを行っており、このステップは非常に重要です。 Tunny はデフォルトで 10 ポイントをサンプリングします。あなたが実行しようとしている最適化にこの数が適しているかどうかを常に考えてください。参考文献にあげている TPE 論文では次の数値を推奨しています。

変数の数 × 11 - 1

十分なサンプリングがないと、KDE は適切に実行されず、次の検索ポイントを効率的に見つけることができません。例として、上記で実行したサンプル数の半分だけを取得した場合の結果を次に示します。

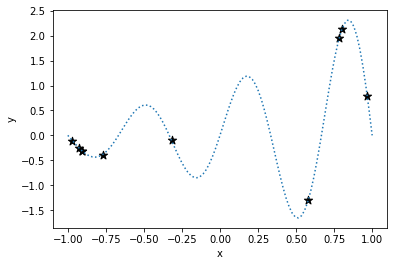
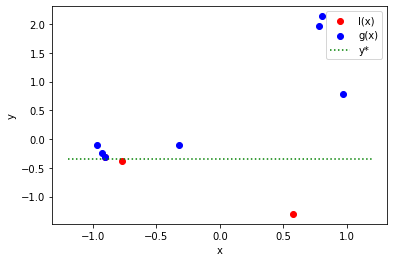
この例では十分にサンプリングされていないため、次の検索ポイントは x=-0.434 と計算されます。これは、大域的最適解が存在する x=0.5 付近の値とはまったく異なります。

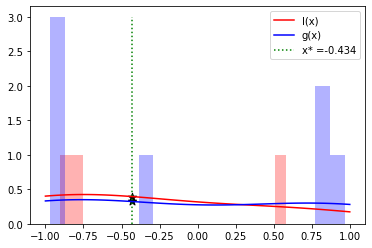
適度な数をサンプリングしないと適切に次の探索点を求める計算が出来ず、最適化がうまくすすまないことに注意してください。